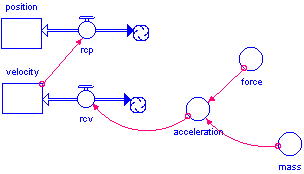
Students should be familiar with STELLA and have built other models prior to this one. It is particularly important that they have built a basic force model and manipulated it to understand the effects on acceleration when either mass or force is varied. The models in this unit simple add other values that can be used to calculate the force. Of course, the force is now a changing force and students should be made aware of this difference between the basic force model and the models of oscillating systems.

Guide the students in a discussion of what needs to be added to this model so that it will represent a horizontal spring. Students should be able to offer that they need a converter for the spring constant and that the position stock needs to be connected to the force converter since the restoring force of a spring depends on the position away from equilibrium (rest). Discuss with the students that the easiest position to define as rest position would be zero, so they will also need to choose an initial position other than 0 to put in the position stock. Finally, because they will be looking at fairly rapid changes over time, they should change the duration of the model to 2 seconds, the DT to 0.02 and the integration method to Runge-Kutta 4.

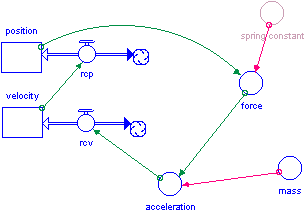
Students should verify the accuracy of the model by entering their experimentally determined spring constant and the mass they used to get the period of the oscillating system into the model. They should then create a graph of position versus time and run the model. They can compare the period of the spring they determined experimentally with that produced by the model. Students should be guided into a realization that this is only a first step in determining the validity of the model.

Once the students have a model which fairly accurately reproduces their experiment, they should use the model to investigate the effect of the mass and the spring constant on the period. If students have not had much experience with manipulating variables, teachers may want to remind them to change only one variable at a time. Alternatively, the teacher could use this opportunity to assess student skills in performing simple investigations with more than one variable. In either case, students should keep a data table of the values they tried for the mass and the spring constant and the period each test run produced. Students should be encouraged to do multiple trials where each is varied, since they do not know if the dependence is linear or non-linear.Students should be asked to describe the relationships they have discovered in a qualitative manner.

For schools where there will be collaboration with a math class, each student or pair of students should be assigned a particular mass and spring constant, create a table for position vs. time, run the model for these values and save the results as a text file for analysis by the math class. (See Mathematics Section).

Students should take their model-produced values and graphically determine how the mass and the spring constant affect the period. Again, the amount of guidance required by the teacher will depend on the previous experiences of the students. If they are familiar with power regression, they should be able to determine that the period is proportional to the square root of the mass and the square root of the inverse of the spring constant.

• Student Preconceptions

  There are many velocity and acceleration preconceptions held by students which can be addressed by the study of oscillating systems (See Preconceptions Section). Teachers who are interested in addressing these should have the students look at velocity and acceleration vs. time graphs as well as the position vs. time graph. Students should especially note the position of the mass on the spring when the mass has maximum velocity and when it has maximum acceleration.

• Changing Force

  In addition, teachers could have the students graph force vs. time and discuss with the class the nature of the restoring force. Emphasis should be placed on the fact that the force is changing and that it is at its maximum when the mass on the spring is farthest from equilibrium.

• Systems

  Teachers who are interested in having students develop a better understanding of systems might discuss the feedback loop which is present in this model (traced with the green arrows in the diagram above).They might also want to discuss how no element in the system possesses the property of oscillation, but rather the oscillation arises as a property of the interaction of the elements of the model. (See AAAS Benchmarks - Common Themes).

NOTES:

1. A series of activities for building other models, including the basic force model can be found at the Maryland Virtual High School site.
2. The spring constant converter is a different color from the other icons to show similarities between models. Teachers who choose to have students build or use the models of the pendulum, the vibrating bar or the tuning fork, will note that in those diagrams, the icons of the basic force model remain the same color and the variables and constants which are added to add specificity to the model are of another color. It is hoped that students will see that not only do these different mechanical systems produce similar behaviors; they can also be represented by very similar models.
3. There is no student worksheet for this activity. The students only need to make a few changes to the model which should be discussed as a class. The students should generate their own data tables.