Model/Concept Extensions

 

Mass attached to a vertical spring

Insert image here Hooke’s law for a spring (F = -kx) is valid for vertical springs. However, there is the additional force of weight acting on the mass. Expand your existing model of a mass attached to a horizontal spring to model a mass attached to a vertical spring.

Create and investigate a working model for the oscillating mass. What factors affect the period? How do they affect it? What factors do not affect the period?

 

Hydrometer floating in a liquid

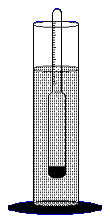The restoring force for a floating object is –g*r*A*y. Where g is the acceleration due to gravity.r is the density of the liquid. A is the cross sectional area. And y is the distance above or below the normal floating layer. There is the additional force of weight acting on the mass.

Create and investigate a working model for the oscillating hydrometer.

What factors affect the period?

 

A simple pendulum

The restoring force comes from the Tension in the string. However the direction of the Tension changes as the pendulum swings. The motion can be modeled if you find the x-component of the Tension. Hence the restoring force will be equivalent to the Tension * Sin(q , Where qis the angle between the Pendulum string and the equilibrium position. Furthermore Sin(q) equals opposite/hypotenuse which is equivalent to x-position/length of string.

Create and investigate a working model for the oscillating pendulum. What factors affect the period? How do they affect it? What factors do not affect the period?

 

A tuning fork

The restoring force of a struck tuning fork is:

The YM (Young’s Modulus) for aluminum is 7x107. Thickness is measured in the direction of oscillation in m. Width is measured perpendicular to the direction of oscillation in m. Length is measured from top to bottom of tine not the entire length of the fork.

Create and investigate a working model for an aluminum tuning fork. What factors affect the period? How do they affect it? What factors do not affect the period?

 

A metal bar fixed at one end

The restoring force for the vibrating bar is: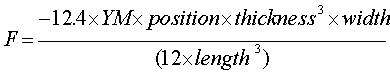

The YM (Young’s Modulus) for aluminum is 7x107. Thickness is measured in the direction of oscillation in m. Width is measured perpendicular to the direction of oscillation in m. Length is measured from oscillating end to clamped end of the bar.

Create and investigate a working model for a vibrating metal bar fixed at one end. What factors affect the period? How do they affect it? What factors do not affect the period?

 

A marble in a circular glass bowl

The restoring force comes from the Normal force acting on the marble. However the direction of the Normal force changes as the marble oscillates. The motion can be modeled if you find the x-component of the Normal force. Hence the restoring force will be equivalent to the Normal Force * Sin(q), Where q is the angle between the extension of the normal force and a radius of the circle that goes through the bottom of the bowl. Furthermore Sin(q) equals opposite/hypotenuse which is equivalent to x-position/ radius of the bowl.

Create and investigate a working model for a marble oscillating in a circular bowl. What factors affect the period? How do they affect it? What factors do not affect the period?