|

|
Using Computation and Communication to Solve Problems
|
|
What is the difference between serial computing and
parallel computing? What does a supercomputer do? Recently, 52 Montgomery Blair High School
students learned the answers to those questions when five professors from the
fields of computer science, math and physics came to Blair to demonstrate LittleFe, a portable, 6-processor parallel computer.
Supercomputers are valuable tools for many scientific and engineering
problems such as weather forecasting, protein folding, genomic sequencing,
and even potato chip packaging! Supercomputers achieve their high speeds by
splitting a problem into parts that can be solved simultaneously; hence the
name, parallel computing.
|

LittleFe, a 6 node, 1GHz, 512MB, x86
unit
|
|

Montgomery Blair
High School students
|
Paul Gray from the University of Northern
Iowa illustrated the difference between serial
and parallel processing by asking the students to imagine how long it would
take them to introduce themselves to the group one at a time. That would be
an example of serial processing. Then he invited all 52 of them to say their
names all at once. Although the resulting noise was unintelligible, it was
fast. Parallel processing requires strategies that result in fast and intelligible
results.
|
|
Using a dart board simulation as an example, Dave Joiner
from Kean University
in New Jersey
showed how a problem could be divided in parts with each part assigned to a
different processor. For the 6 processors of LittleFe,
the dart board was divided into 6 pie-shaped wedges into which random hits
were made. To calculate the score for a random game of darts, the results
from each processor are then shared.
|
|

The dart board
|

A one-sixth slice
|
|
|
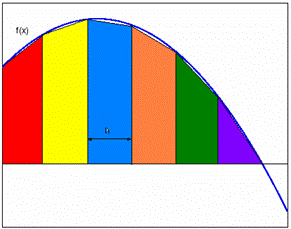
Area under a curve
|
Parallel processing can also be used to find the area
under a curve in lightning-fast speed. Tom Murphy from Contra
Costa College
in California
demonstrated how a region under a curve could first be divided into six
regions, each given to a separate processor. Each processor can then
subdivide its parts into a thousand or more smaller trapezoids depending on
the accuracy needed in the result. After each processor calculates the sum of
the trapezoids assigned to it, the six sums can be added together to provide
the total area. Consequently, the sum when calculated by six processors can
be found in 1/6th the amount of time it would take for a single
processor.
|
|
Not all problems can be divided in such a way as to
achieve this speed-up advantage. Charlie Peck from Earlham
College in Indiana showed the group that while some
problems, like area under a curve, can be divided into 6 independent parts;
other problems have parts that are necessarily interdependent. He used
protein folding as an example. In protein folding, the shape of the protein
is partially determined by whether its amino acids are attracted to water
(hydrophilic) or repelled by water (hydrophobic). In this simulation, an
amino acid necklace is placed in a water bath that is divided into 6 slices,
one per processor, and distant groups of water molecules as treated as one
big molecule to improve performance. Since amino acids in one slice are
attracted to or repelled by water molecules in all six slices, communication
between the slices occurs frequently. Solving the problem in parallel across
six processors significantly speeds up the process, but less than the ideal
1/6th factor because of the added communication.
|
|
Top View Side View
GalaxSee
|
What do galaxies and protein folding have in common?
Both are n-body problems, meaning that every object is affected by every
other object. In galaxies, those objects are stars, each of which affects the
others through gravitation and rotation. Dave Joiner demonstrated the GalaxSee simulation which showed a cluster of stars
forming a disc-like galaxy when rotation is present. He explained that studies
have shown that gravitation and rotation are not sufficient to explain all spiral
galaxies, and that models of collisions can be used to extend our knowledge
of galactic structure.
|
|
During a question and answer session after the
presentation, Henry Neeman, Director of the OU
Supercomputing Center for Education and Research (OSCER) in Oklahoma spent time explaining to
individual students the role of high performance computing in modern science
and the struggle between the demands of computation and communication in
optimizing code for supercomputers.
|

Q&A Session
|
|

LittleFe Components
|
The students who attended this presentation were shown
the power of parallel computing and the diverse problems to which
supercomputing may be applied. At a LittleFe
construction demonstration, students learned about the component parts and
helped put one together. The diagram shows the six 512MB processor blades and
the 1GB drive blade (lower right hand corner) that were used in the
construction of a LittleFe.
|
|

|
The Bootable Cluster CD developed by Paul Gray at UNI
may be used to turn a collection of networked PCs into a parallel computer.
|
|
The LittleFe
Team
First
Row (left to right)
Kristina
Wanous, University
of Northern Iowa
Susan
Ragan, Maryland
Virtual High School
Paul
Gray, University
of Northern Iowa
Henry Neeman, OU Supercomputing Center for Education and
Research
Jared Ribble, Crownpoint Institute of
Technology
Tom
Murphy, Contra Costa College
Back
Row (left to right)
Charlie
Peck, Earlham College
Alex
Lehmann, Earlham
College
Chris Yazzie, Crownpoint Institute of
Technology
Dave
Joiner, Kean University
Scott
Lathrop, TeraGrid
|

|
|
|
|
|










