|
|
Vensim Version
|
STELLA Version
|
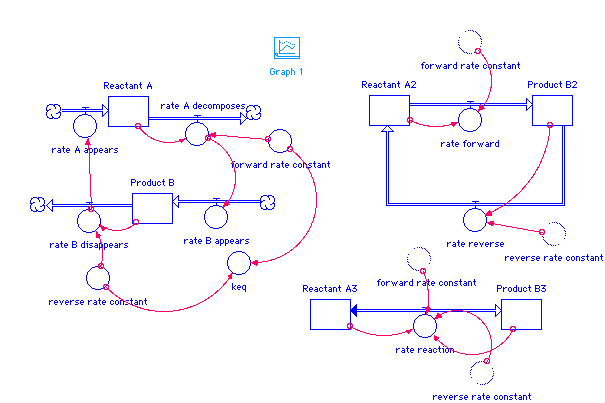
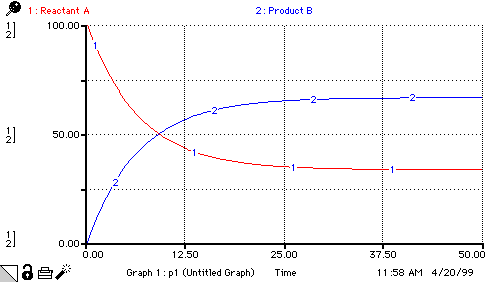
Product_B(t) = Product_B(t - dt) + (rate_B_appears - rate_B_disappears) * dt INIT Product_B = 0 INFLOWS: rate_B_appears = rate_A_decomposes OUTFLOWS: rate_B_disappears = Product_B*reverse_rate_constant Product_B2(t) = Product_B2(t - dt) + (rate_forward - rate_reverse) * dt INIT Product_B2 = 0 INFLOWS: rate_forward = forward_rate_constant*Reactant_A2 OUTFLOWS: rate_reverse = reverse_rate_constant*Product_B2 Product_B3(t) = Product_B3(t - dt) + (rate_reaction) * dt INIT Product_B3 = 0 INFLOWS: rate_reaction = forward_rate_constant*Reactant_A3-reverse_rate_constant*Product_B3 Reactant_A(t) = Reactant_A(t - dt) + (rate_A_appears - rate_A_decomposes) * dt INIT Reactant_A = 100 INFLOWS: rate_A_appears = rate_B_disappears OUTFLOWS: rate_A_decomposes = Reactant_A*forward_rate_constant Reactant_A2(t) = Reactant_A2(t - dt) + (rate_reverse - rate_forward) * dt INIT Reactant_A2 = 100 INFLOWS: rate_reverse = reverse_rate_constant*Product_B2 OUTFLOWS: rate_forward = forward_rate_constant*Reactant_A2 Reactant_A3(t) = Reactant_A3(t - dt) + (- rate_reaction) * dt INIT Reactant_A3 = 100 OUTFLOWS: rate_reaction = forward_rate_constant*Reactant_A3-reverse_rate_constant*Product_B3 forward_rate_constant = .1 keq = forward_rate_constant/reverse_rate_constant reverse_rate_constant = .05