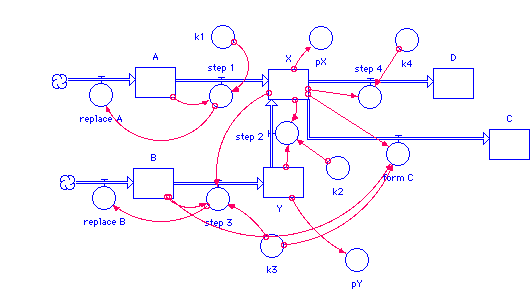
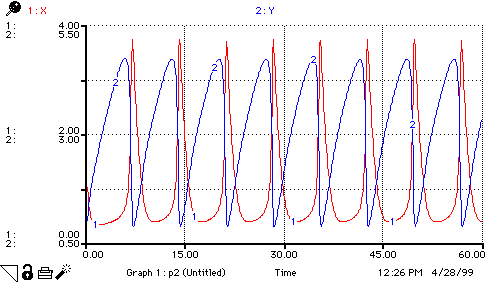
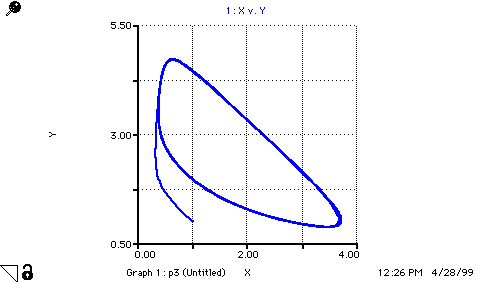
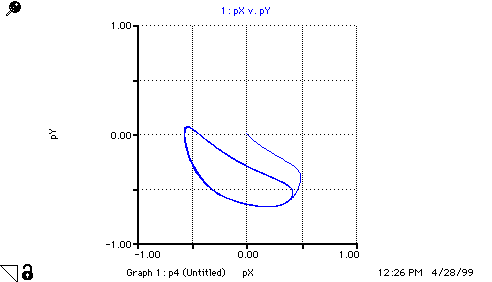
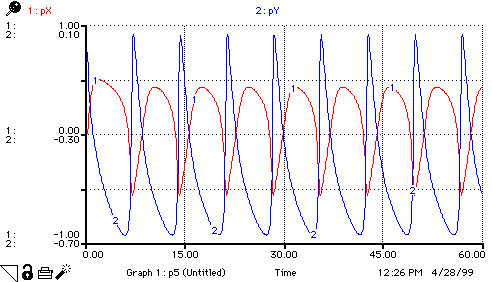
A(t) = A(t - dt) + (replace_A - step_1) * dt
INIT A = 1
replace_A = step_1
step_1 = k1*A
B(t) = B(t - dt) + (replace_B - step_3) * dt
INIT B = 3
replace_B = step_3
step_3 = k3*B*X
C(t) = C(t - dt) + (form_C) * dt
INIT C = 0
form_C = k3*B*X
D(t) = D(t - dt) + (step_4) * dt
INIT D = 0
step_4 = k4*X
X(t) = X(t - dt) + (step_1 + step_2 - step_4 - form_C) * dt
INIT X = 1
step_1 = k1*A
step_2 = k2*(X^2)*Y
step_4 = k4*X
form_C = k3*B*X
Y(t) = Y(t - dt) + (step_3 - step_2) * dt
INIT Y = 1
step_3 = k3*B*X
step_2 = k2*(X^2)*Y
k1 = 1
k2 = 1
k3 = 1
k4 = 1
pX = -LOG10(X)
pY = -LOG10(Y)

Time Specs