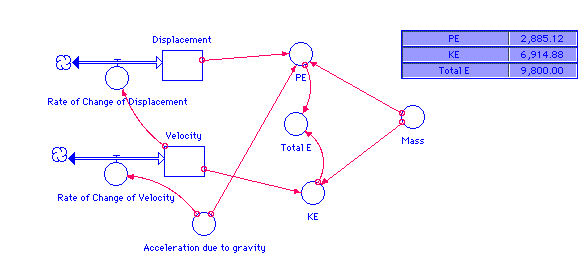
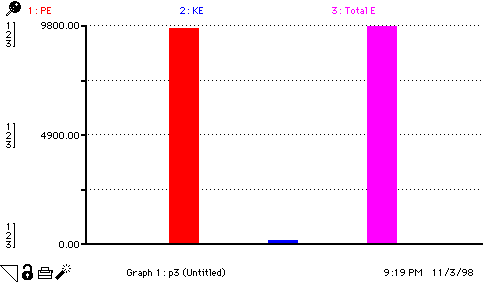
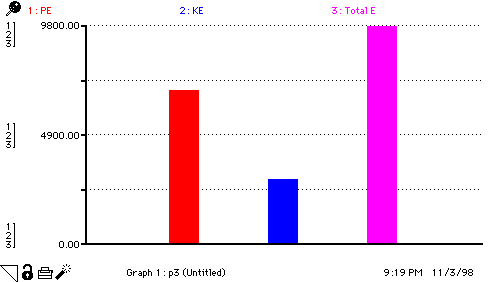
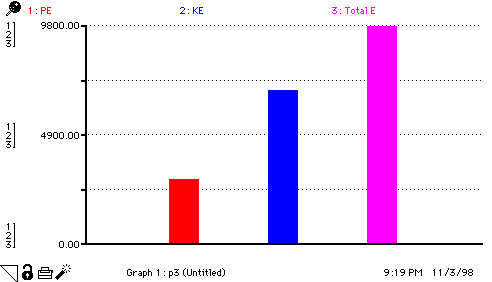
This is a simple adjustment of the free fall model to show conservation of energy. The three graphs which appear here are "snapshots" from one run of the model, taken at 1.75 s, 8 s and 12 s.
|
|
Vensim Version
|
STELLA Version
|
Displacement(t) = Displacement(t - dt) + (Rate_of_Change_of_Displacement) * dt INIT Displacement = 1000 Rate_of_Change_of_Displacement = Velocity Velocity(t) = Velocity(t - dt) + (Rate_of_Change_of_Velocity) * dt INIT Velocity = 0 Rate_of_Change_of_Velocity = Acceleration_due_to_gravity Acceleration_due_to_gravity = -9.8 KE = .5*Mass*Velocity^2 Mass = 1 PE = Mass*ABS(Acceleration_due_to_gravity)*Displacement Total_E = PE+KE
Time Specs
Range: 0-12, dT = 0.25, Integration Method = Runge-Kutta 4
