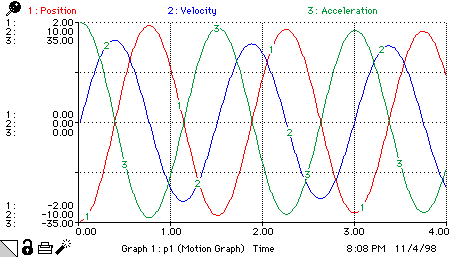
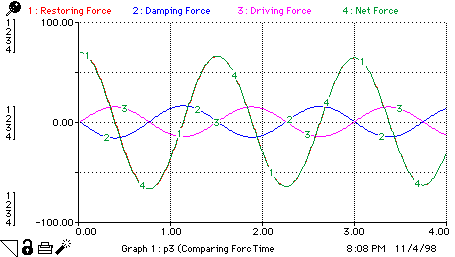
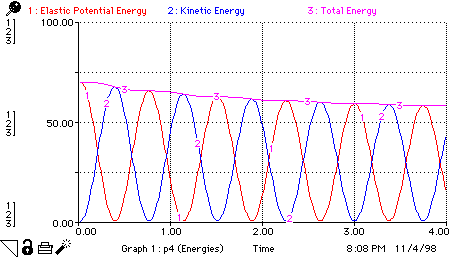
|
|
Vensim Version
|
STELLA Version
|
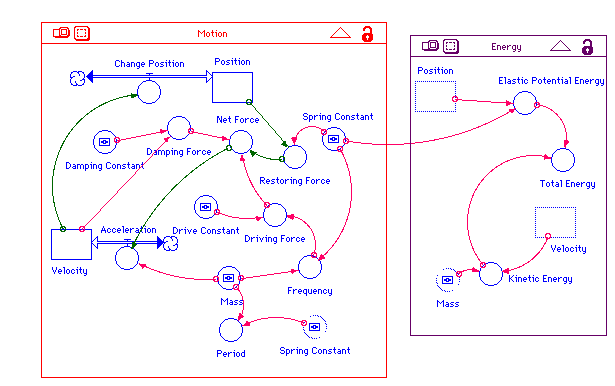
Elastic_Potential_Energy = .5 *Spring_Constant*Position^2 Kinetic_Energy = .5*Mass*Velocity^2 Total_Energy = Elastic_Potential_Energy+Kinetic_Energy Position(t) = Position(t - dt) + (Change_Position) * dt INIT Position = -2 Change_Position = Velocity Velocity(t) = Velocity(t - dt) + (Acceleration) * dt INIT Velocity = 0 Acceleration = Net_Force/Mass Damping_Constant = 2 Damping_Force = -Damping_Constant*Velocity Drive_Constant = 15 Driving_Force = Drive_Constant*sin(TIME*Frequency) Frequency = SQRT(Spring_Constant/Mass) Mass = 2 Net_Force = Restoring_Force+Damping_Force+Driving_Force Period = 2*PI*SQRT(Mass/Spring_Constant) Restoring_Force = -Spring_Constant*Position Spring_Constant = 35