During the study of 2-dimensional motion, students are asked to build a model of projectile motion. The comparative graph (graph 2) shows the effect of the launch angle (30, 45 or 60 degrees) on the path of the projectile. After building the basic model, students can add other factors such as drag, a wind in the horizontal direction, or an initial positive launch height. 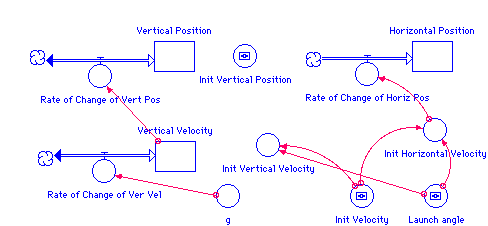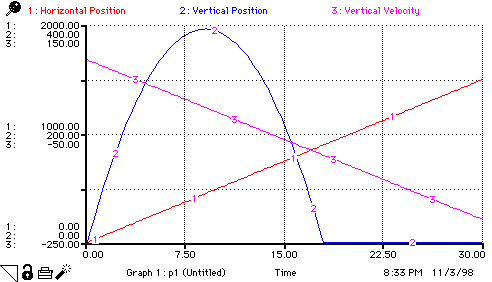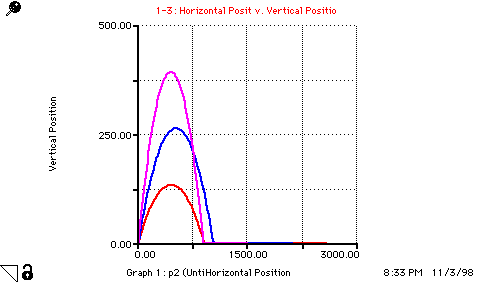THE MODEL Vensim Version Vensim PLE Software Right-click to download the model Projectile Motion Vensim STELLA Version isee Player Software Right-click to download the model Projectile Motion STELLA PC Projectile Motion STELLA Mac [Diagram Level | Equations Level | Graphs ] Horizontal_Position(t) = Horizontal_Position(t - dt) + (Rate_of_Change_of_Horiz_Pos) * dt INIT Horizontal_Position = 0 Rate_of_Change_of_Horiz_Pos = Init_Horizontal_Velocity Vertical_Position(t) = Vertical_Position(t - dt) + (Rate_of_Change_of_Vert_Pos) * dt INIT Vertical_Position = Init_Vertical_Position Rate_of_Change_of_Vert_Pos = Vertical_Velocity Vertical_Velocity(t) = Vertical_Velocity(t - dt) + (Rate_of_Change_of_Ver_Vel) * dt INIT Vertical_Velocity = Init_Vertical_Velocity Rate_of_Change_of_Ver_Vel = g g = -9.8 {m/s^2} Init_Horizontal_Velocity = Init_Velocity*COS(Launch_angle*PI/180) Init_Velocity = 100 {m/s} Init_Vertical_Position = 0 Init_Vertical_Velocity = Init_Velocity*SIN(Launch_angle*PI/180) Launch_angle = 30 Time Specs Settings Standard:Range: 0-30 ; dt = 0.25; Integration Method = Euler's

Home | Contact | Site Map | Search