|
|
Vensim Version
|
STELLA Version
|
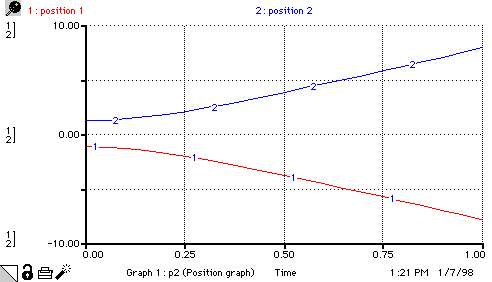
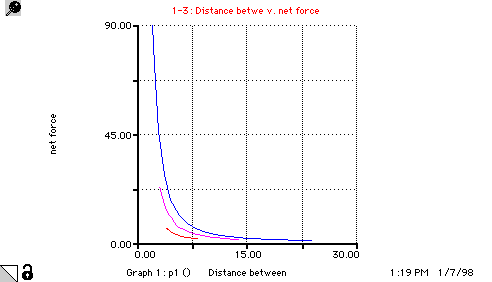
position_1(t) = position_1(t - dt) + (rate_of_change_of_pos_1) * dt INIT position_1 = Init_position_1 rate_of_change_of_pos_1 = velocity_1 position_2(t) = position_2(t - dt) + (rate_of_change_of_pos_2) * dt INIT position_2 = Init_position_2 rate_of_change_of_pos_2 = velocity_2 velocity_1(t) = velocity_1(t - dt) + (rate_of_change_of_vel_1) * dt INIT velocity_1 = 0 rate_of_change_of_vel_1 = accel_1 velocity_2(t) = velocity_2(t - dt) + (rate_of_change_of_vel_2) * dt INIT velocity_2 = 0 rate_of_change_of_vel_2 = accel_2 accel_1 = -net_force/mass_1 accel_2 = net_force/mass_2 charge_1 = 1e-4 charge_2 = 1e-4 Distance_between = position_2-position_1 Init_position_1 = -1 Init_position_2 = 1 mass_1 = 1 mass_2 = 1 net_force = 9e9*(charge_1*charge_2)/(Distance_between)^2
Time Specs Settings
Range: 0-1; dt = 0.01; Integration Method = Runge-Kutta 4