Friction Model  

This is another model that students can use to explore Newton's second law. Students first identify friction as the opposing force and a "push" as the applied force. Through their work with the model, they try to reproduce the conditions of an experiment performed in class.

THE MODEL
Vensim Version STELLA Version

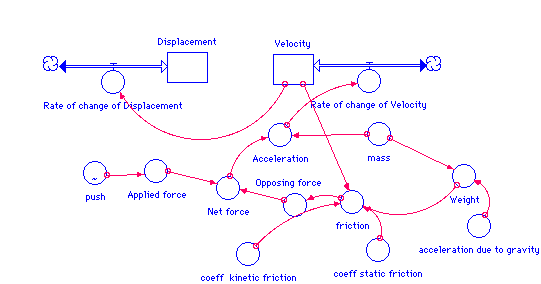
[Diagram Level | Equations Level | Graphs ]

 Displacement(t) = Displacement(t - dt) + (Rate_of_change_of_Displacement) * dt
INIT Displacement = 0 {m}
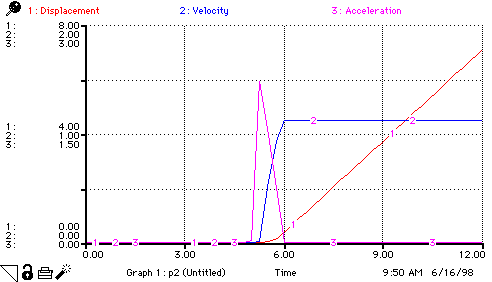
Rate_of_change_of_Displacement = Velocity
Velocity(t) = Velocity(t - dt) + (Rate_of_change_of_Velocity) * dt
INIT Velocity = 0 {m/s}
Rate_of_change_of_Velocity = Acceleration
Acceleration = Net_force/mass
acceleration_due_to_gravity = -9.8 {m/s^2}
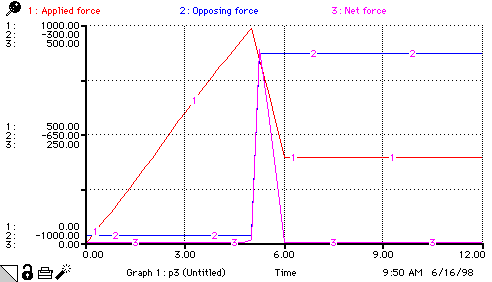
Applied_force = push
coeff_static_friction = 0.5
coeff__kinetic_friction = 0.2
friction = IF Velocity> 0 THEN coeff__kinetic_friction*Weight ELSE coeff_static_friction*Weight
mass = 200 {kg}
Net_force = IF (ABS(Applied_force)>ABS(Opposing_force)) THEN (Applied_force+Opposing_force) ELSE 0
Opposing_force = friction
Weight = mass*acceleration_due_to_gravity
push = GRAPH(time) (0.00, 0.00), (1.00, 190), (2.00, 390), (3.00, 605), (4.00, 800), (5.00, 985), (6.00, 392), (7.00, 392), (8.00, 392), (9.00, 392), (10.0, 392), (11.0, 392), (12.0, 392)
Time Specs Settings
Standard: Range: 0-12 ; dt = 0.25 ; Integration Method = Euler's

Home | Contact | Site Map | Search