|
|
Vensim Version
|
STELLA Version
|
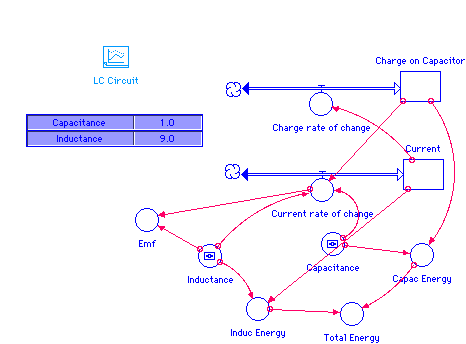
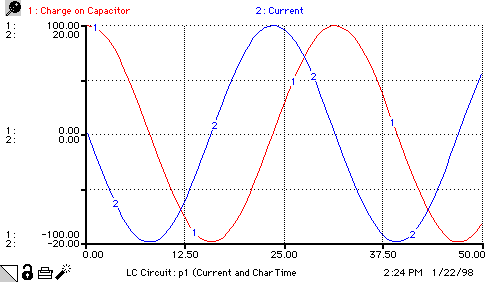
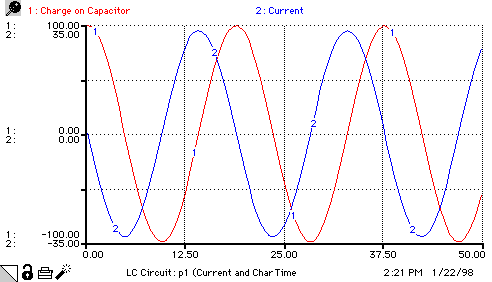
Charge_on_Capacitor(t) = Charge_on_Capacitor(t - dt) + (Charge_rate_of_change) * dt
INIT Charge_on_Capacitor = 100
Charge_rate_of_change = Current
Current(t) = Current(t - dt) + (Current_rate_of_change) * dt
INIT Current = 0
Current_rate_of_change = -Charge_on_Capacitor/(Inductance*Capacitance)
Capacitance = 1
Capac_Energy = Charge_on_Capacitor^2/(2*Capacitance)
Emf = -Inductance*Current_rate_of_change
Inductance = 9
Induc_Energy = (Inductance*Current^2)/2
Total_Energy = Capac_Energy+Induc_Energy
Time Specs
Range: 0 - 50, dT = 0.5, Integration Method: Runge-Kutta 4