|
|
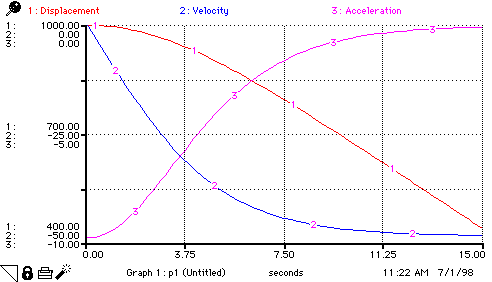
Vensim Version
|
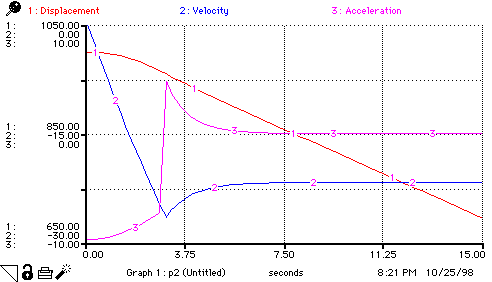
STELLA Version
|
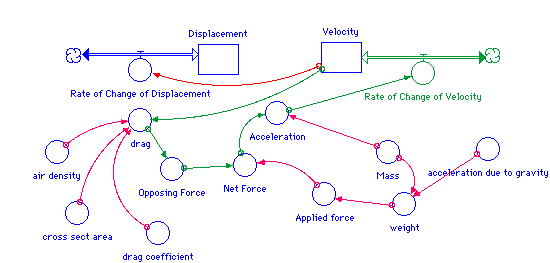
Displacement(t) = Displacement(t - dt) + (Rate_of_Change_of_Displacement) * dt
INIT Displacement = 1000 {m}
Rate_of_Change_of_Displacement = Velocity
Velocity(t) = Velocity(t - dt) + (Rate_of_Change_of_Velocity) * dt
INIT Velocity = 0 {m/s}
Rate_of_Change_of_Velocity = Acceleration
Acceleration = Net_Force/Mass
acceleration_due_to_gravity = -9.8 {m/s^2}
air_density = 1.16 {kg/m^3}
Applied_force = weight
cross_sect_area = if time < 3 then 0.5 {m^2} else 2.5
drag = 0.5*drag_coefficient*air_density*cross_sect_area*Velocity^2
drag_coefficient = 1
Mass = 70 {kg}
Net_Force = Applied_force+Opposing_Force
Opposing_Force = drag
weight = Mass*acceleration_due_to_gravity
Time Specs Settings
Range: 0 -15 ; dt = 0.25 ; Integration Method = Euler's