

[Rate of mass B flow into V]=[Rate of mass B flow out of V] + [Rate of mass B loss due to mass transfer from V] + [Rate of mass B loss due to chemical reaction within V] + [Rate of accumulation of mass B in V] (eq. 1)
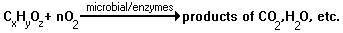
This equation simplifies the biological removal processes of organic pollutants, CxHyOz, in streams. The organic impurities require an amount of of oxygen, O2, measured as an "oxygen demand". The biochemical conversion of 1 g of "oxygen demand" organic matter requires 1 g of molecular oxygen. The removed oxygen must be replaced by reoxygenation which occurs through the contact between the water's surface and the atmosphere. The concentration of oxygen in the stream water is called dissolved oxygen. Factors which affect it include temperature, concentration of all organic wastes, and water's surface areas. However, the concentration of the organic impurities can be so great that it will reduce the concentration of dissolved oxygen. When the oxygen concentration falls below the minimum requirements of marine life, the diversity of organisms in the stream will be reduced. Therefore, some discharge of organic waste into streams is acceptable, but it must be limited to the stream's capacity to assimilate.
Deoxygenation and Reoxygenation Mathematical
Theory:
The classical work of Streeter Phelps in 1925 presented a
mathematical analysis of the organic waste and oxygen content in water
known as the oxygen sag. Consider an idealized stream: has a volume V of
water, moves at the average velocity v, contains an oxygen concentration
rA and organic chemical B of concentration rB. This volume V is located a
distance L downstream from the single organic waste point of entry. Only
two mechanisms, biochemical oxydation and interphase mass transfer of
oxygen are occurring within the water. According to eq. 1, the organic
material B can be written as:
The rate disappearance of B is assumed to be a first order rate equation:
where k'''B is the rate constant. The negative sign in front of the rate symbol denotes the disappearance of B.
Combining eq. 3 and eq. 4, we can have:
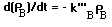
Oxygen, component A, enters the water through water's surface area Azx. The interphrase flux rate is:
where:
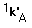 is mass transfer coefficient of oxygen
is mass transfer coefficient of oxygen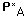 is the concentration of oxygen upstream from
the organic waste point of entry
is the concentration of oxygen upstream from
the organic waste point of entry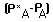 is the oxygen deficit
is the oxygen deficit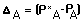
According to eq. 1, the material balance of oxygen can be written as:
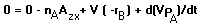
Where Azx is the interface area of air and water contact for a constant
volume V.
Substitute eq. 6 and eq. 7 into eq. 8 to obtain:
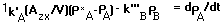
With the definition of oxygen deficit in eq. 7, eq. 9 can be expressed as:
(assuming a constant stream temperature)
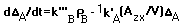
Note:
k'''B is the oxygenation coefficient (t-1)Here, the rate of reaeration of oxygen can be examined with equation 5 and 10. If the initial conditions are:
1k'A (Azx/V) is the reaeration coefficient (t-1)
DA = DAøOne can integrate with the initial conditions and combine eq. 5 and eq. 10 to obtain the relationship of oxygen deficit:
pB = pBø
t = 0
h = Azx/V - the depth of river
![DA = {{[k'''B pøB]/[ (1k'A/h) - k'''B]}*{e(-k'''Bt) -
e(1k'At/h)}} + DAøe(-1k'At/h)](./eq11.gif)
Note: This Model came from Chemodynamics by Louis J. Thibodeaux.
[Back]
[