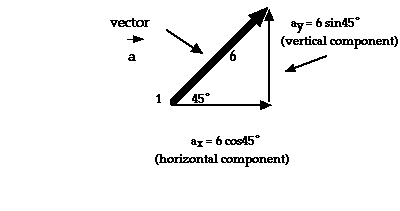
A vector has magnitude and direction. Let's say the vector (force) a has a
magnitude of 6 and a direction of 45 degrees from the horizontal. We represent a
vector as a directed line segment, that is, a line segment pointing in a
particular direction. The length of the segment is the magnitude, in
this case, 6. The direction of the vector, shown by the use of an arrowhead,
is the direction of the quantity, in this case 45 degrees. Using right triangle
trigonometry, we can separate the vector into the two parts shown.
Solving a System of Equations
Let's review the concept of solving a system of equations. If you can
eliminate a variable, you can reduce the problem to a system with two
variables.Then it becomes a familiar situation. Let's proceed through a
system with 3 variables. If there are 3 variables, then there will be 3
equations. Suppose our system is:
2x + 3y - z = -1 *1 -x + 5y + 3z = -10 *2 3x - y - 6z = 5 *3The technique of linear combination that you used on a system with two variables will be used to solve our system. First, we need to choose a variable and eliminate it. This is accomplished by writing two different pairs of equations from the system and using the linear combination method. We will choose x to eliminate. Proceed as follows:
The first pair chosen is the first and second equations of our system. Multiply both sides of *2 by 2 and add the resulting equation to *1. (Thus eliminating the x variable and creating a new equation which we will call *4.)
-2x + 10y + 6z = -20 *2 x 2
2x + 3y - z = - 1 *1
13y + 5z = -21 *4
The second pair chosen is the second and third equations of our system. Multiply *2 by 3
and add the resulting equation to *3. (Again we have eliminated the x variable and we have
created a new equation which we will call *5).
-3x + 15y + 9z = -30 *2 x 3
3x - y - 6z = 5 *3
14y + 3z = -25 *5
Now we have two equations, and we can continue using the process of linear
combination. We now need to eliminate another variable. Let's choose z. We
can accomplish the elimination by multiplying *4 by 3 and *5 by -5 and
then adding them together. ( Yes, we could have multiplied *5 by +5 and
then subtracted the equations.) The result is a linear equation in ONE
variable which we readily solve. Take a look.
39y + 15z = -63 -70y
-15z = 125 -31y = 62
therefore: y = -2
Now we substitute the y value, -2, into *4 (or *5) and gain the value for z.
13(-2) + 5z = -21
-26 + 5z = -21
5z = 5
therefore: z = 1
Hang on! We're almost done! Now all we have to do is substitute the values for y
and z into any one of the original equations , solve for x and viola! We have our solution set!
We will use *1 and proceed as follows.
2x + 3y -z = -1
2x + 3(-2) -(1) = -1
2x - 6 -1 = -1
therefore: 2x = 6
x = 3 (Hooray!)
So, we arrive at the solution set: {3, -2, 1}This process has been used to solve a system in which there are 3 unknowns. Sometimes, there are many more unknowns in a particular problem. When that happens, it's time to turn to technology to solve the equations for us!
Bibliography:
Return to the Bridge Model Main Page