Glucose is the vehicle by which energy gets from digested food to the cells of the body. In Type I diabetes mellitus, insufficient insulin is available to help get glucose out of the blood and into the cells of the body. This activity has been designed so that students can investigate the negative feedback loop between blood glucose and insulin, one of the mechanisms designed to maintain homeostasis in the human body.

TEACHER RESOURCES Teacher Materials Student Activity Student    Assessment Learning    Goals/Standards COMPUTER MODELS Based on a model from Will Glass-Husain, Tucson, AZ STELLA Versions isee Player software Right-click to download the models Part 1 PC Format Part 2 PC Format Part 1 Mac Format Part 2 Mac Format Vensim Version Vensim PLE Software Right-click to download the model Glucose-Insulin Model

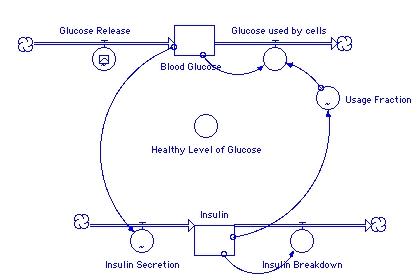
THE MODEL DIAGRAM THE EQUATIONS Blood_Glucose(t) = Blood_Glucose(t - dt) + (Glucose_Release - Glucose_used_by_cells) * dt INIT Blood_Glucose = 6000 {mg} Glucose_Release = GRAPH(time) (0.00, 198), (12.0, 198), (24.0, 198), (36.0, 198), (48.0, 198), (60.0, 198), (72.0, 198), (84.0, 198), (96.0, 198), (108, 198), (120, 198) Glucose_used_by_cells = Blood_Glucose*Usage_Fraction Insulin(t) = Insulin(t - dt) + (Insulin_Secretion - Insulin_Breakdown) * dt INIT Insulin = 9000 {units} Insulin_Secretion = GRAPH(Blood_Glucose) (1000, 0.00), (2000, 15.0), (3000, 85.0), (4000, 190), (5000, 350), (6000, 500), (7000, 665), (8000, 825), (9000, 930), (10000, 975), (11000, 995) Insulin_Breakdown = Insulin/18 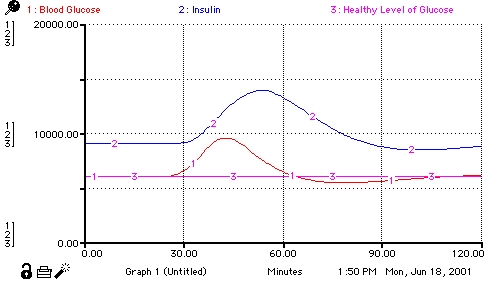Healthy_Level_of_Glucose = 6000 {mg} Usage_Fraction = GRAPH(Insulin) (0.00, 0.0075), (1800, 0.0105), (3600, 0.0145), (5400, 0.019), (7200, 0.0255), (9000, 0.033), (10800, 0.0405), (12600, 0.049), (14400, 0.0545), (16200, 0.0575), (18000, 0.059)

THE OUTPUT

Home | Contact | Site Map | Search