In this activity, students use systems modeling to represent the components of velocity and displacement in two dimensions. They recognize that there is now a displacement in two dimensions, that the velocity at an angle has two components, and that by varying the angle, they can vary the distance traveled in the horizontal direction.

TEACHER RESOURCES Teacher Materials Student Activity Learning    Goals/Standards

COMPUTER MODEL STELLA Version isee Player Software Right-click to download the model Projectile Motion STELLA PC Projectile Motion STELLA Mac Web-based Simulation

COMPUTER MODEL Vensim Version Vensim PLE Software Right-click to download the model Projectile Motion Vensim

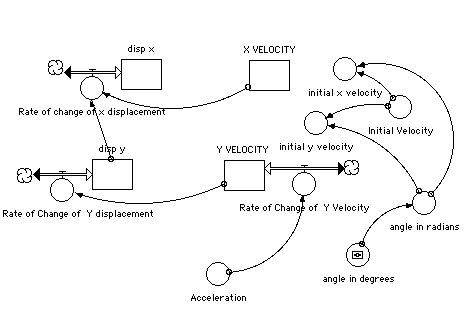
THE MODEL DIAGRAM THE EQUATIONS disp_x(t) = disp_x(t - dt) + (Rate_of_change_of_x_displacement) * dt INIT disp_x = 0 Rate_of_change_of_x_displacement = IF(disp_y>=0.2) then (X_VELOCITY) else 0 disp_y(t) = disp_y(t - dt) + (Rate_of_Change_of__Y_displacement) * dt INIT disp_y = 0 Rate_of_Change_of__Y_displacement = Y_VELOCITY X_VELOCITY(t) = X_VELOCITY(t - dt) INIT X_VELOCITY = initial_x_velocity Y_VELOCITY(t) = Y_VELOCITY(t - dt) + (Rate_of_Change_of__Y_Velocity) * dt INIT Y_VELOCITY = initial_y_velocity Rate_of_Change_of__Y_Velocity = Acceleration Acceleration = -9.8 {m/s/s} 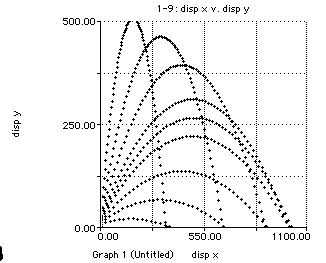angle_in_degrees = 0 angle_in_radians = angle_in_degrees*(PI/180) Initial_Velocity = 100 {m/s} initial_x_velocity = Initial_Velocity*COS(angle_in_radians) initial_y_velocity = Initial_Velocity*SIN(angle_in_radians)

THE OUTPUT

Home | Contact | Site Map | Search