The purpose of this activity is to use a computer simulation to re-create the Rutherford Gold Foil Experiment so that the students can see the likely paths of the alpha particles which were deflected by the nucleus. The students are also able to see the relationship between the atomic number of a nucleus and the paths of the deflected particles.

TEACHER RESOURCES Teacher Materials Student Activity Learning Goals/Standards COMPUTER MODEL Based on a model from Hans Niedderer and Horst Schecker at the University of Bremen in Bremen, Germany PC Format Mac Format STELLATM software AUTHORS Charlotte Trout   Williamsport HS   Williamsport, MD

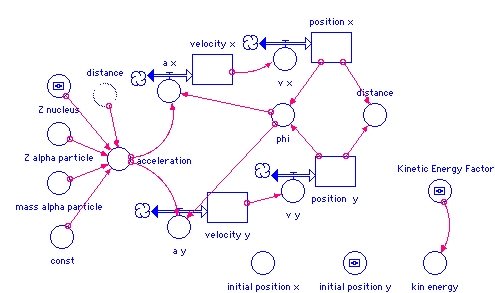
THE MODEL DIAGRAM THE EQUATIONS position_x(t) = position_x(t - dt) + (v_x) * dt INIT position_x = initial_position_x v_x = velocity_x position__y(t) = position__y(t - dt) + (v_y) * dt INIT position__y = initial_position_y v_y = velocity_y velocity_x(t) = velocity_x(t - dt) + (a_x) * dt INIT velocity_x = SQRT(2*kin_energy/mass_alpha_particle) a_x = acceleration*COS(phi) velocity_y(t) = velocity_y(t - dt) + (a_y) * dt INIT velocity_y = 0 a_y = -acceleration*SIN(phi) acceleration = -const*Z_alpha_particle*Z_nucleus*     (1.6e-19)^2/distance^2/mass_alpha_particle const = 1/(4*PI*8.85E-12) distance = SQRT(position_x^2+position__y^2) 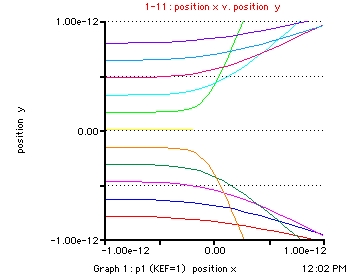initial_position_x = -1e-12 initial_position_y = .01e-12 Kinetic_Energy_Factor = 1 kin_energy = Kinetic_Energy_Factor*1e6 {eV} * 1.6e-19 {As} mass_alpha_particle = 4*1.66e-27 {kg} phi = If position__y>=0 then SQRT((ARCTAN(position__y/position_x))^2)     ELSE - SQRT((ARCTAN(position__y/position_x))^2) Z_alpha_particle = 2 Z_nucleus = 79

THE OUTPUT

Home | Contact | Site Map | Search