Mary Ellen Verona
Maryland Virtual High School of Science and Mathematics
Silver Spring, Maryland 20901
Based on a similar problem from the 2nd Scientific American Book of Mathematical Puzzles and Diversions by Martin Gardner
It's your planning period and you've just poured yourself a cup of coffee and taken cream from the refrigerator when the fire alarm rings. Should you add the cream to the coffee now or wait till you get back? Which method will result in a warmer cup of coffee upon your return? The answer to this problem is not intuitive to most of us. MVHS students were asked to solve this problem under the following conditions:
Given 250 grams of coffee at 90 degrees Celsius and 50 grams of cream at 10 degrees Celsius in a room whose temperature is
20 degrees Celsius.
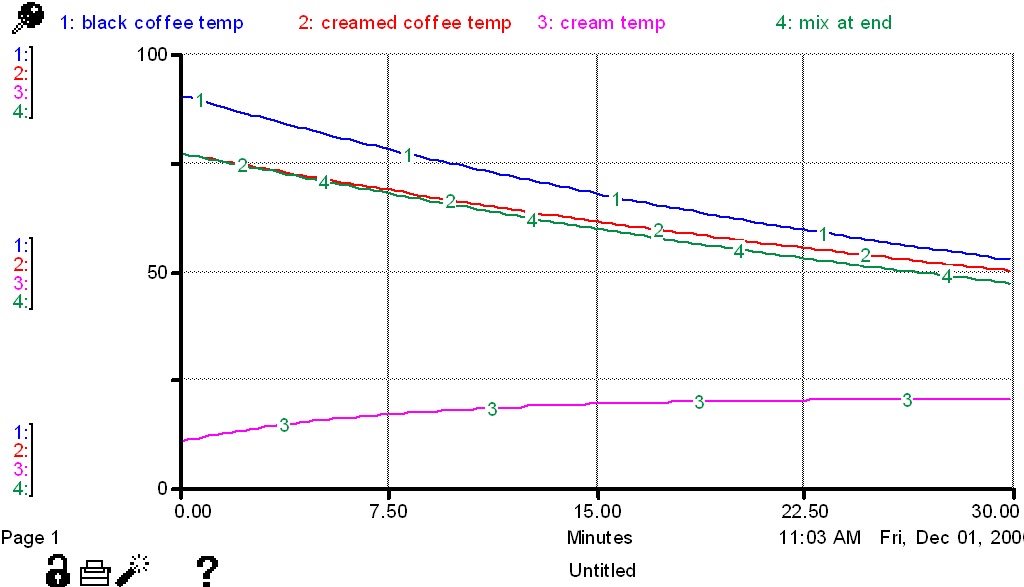
Case 1: Cream is mixed with coffee immediately, creamed coffee held for 30 minutes.
Case 2: Cream and coffee are held at room temperature for 30 minutes and then mixed.
In which case is the creamed coffee hotter? What is the temperature in each case? Assume
that the temperature of the black coffee will be approximately 52 degrees after 30 minutes
at room temperature.
Note: Cooling is inversely proportional to mass and directly proportional to the temperature difference between the substance and its environment.
It is assumed that 1 gram of coffee,
cream, and creamed coffee at the same temperature will cool at the same rate (have the same specific heat).
It is not necessary that you understand specific heat to solve this problem. The given temperature
of black coffee after 30 minutes determines a missing factor.
Students from six high schools submitted their answers. Two high schools took an experimental approach and used CBL's
to find that the mixed coffee was hotter. But the difference in coffee temperature at one school was 7 degrees Celsius less than the
difference at the other school. What outside factors might account for this difference?
Students at the other schools tried modeling the problem. First, they used a weighted average to determine the
initial temperature of the creamed coffee. Then they found the cooling rate for the black coffee by using the
given information that black coffee would drop from 90 to 52 degrees Celsius in 30 minutes. They applied
this same rate to the cream and creamed coffee in spite of the differences in mass. This error produced an incorrect answer.
Modeling software, such as STELLA or a spreadsheet, can be used to model this problem effectively.
In the STELLA model shown,
the cream, creamed coffee, and coffee stocks are initialized to 10, 87.67, and 90
degrees Celsius, respectively. Air temp is held constant at 20 degrees Celsius because the volume of air in the room
is so much greater than the volume of the liquids. At each time step, the stocks representing the
temperatures of the liquids change depending on the rate of the temperature increase or decrease.
Each rate equation is of the form coefficient*temp difference/mass.
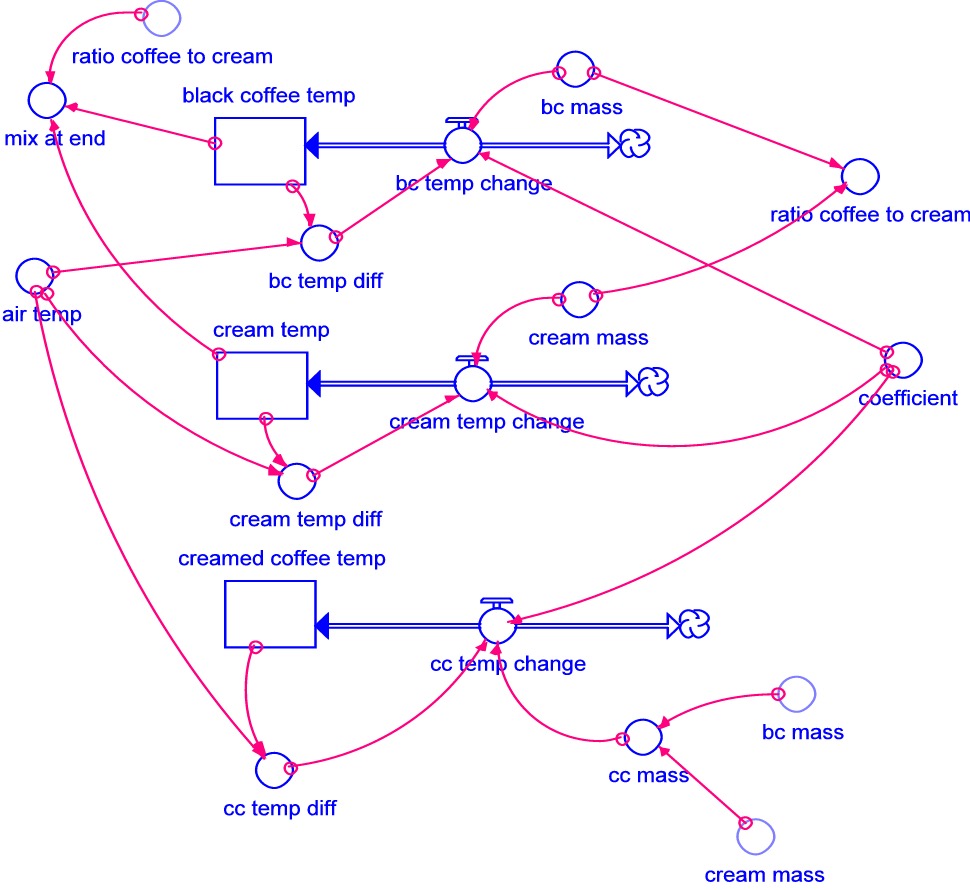
A trial and error method can be used to find the value of the coefficient. We know that the black coffee cools to 52 degrees in 30 minutes. Trying values of 1 and 10 for the coefficient, we find that 1 results in too little cooling and 10 results in too much. It doesn't take long to settle on the value of 6.5.