In order to investigate real world problems through the vehicle of computational science, students must apply their knowledge and skills in science, mathematics, and problem-solving in a structured, organized manner. MVHS teachers, who represent all areas of science, desired a non-discipline-specific problem through which they could identify their students' problem-solving strengths and weaknesses. The snow task was developed in response to that need.

The teachers were asked to assign students in heterogeneous groups of four and to select the tools that would be available to them (e.g. paper and pencil, graph paper, calculators, spreadsheet, modeling software, word processor). Teachers varied in the tools they allowed their students to use. Tim Altaner, who used the task in a computer applications class, required that the students use modeling software; while Charlotte Trout gave her chemistry and physics classes freedom to select the tools of their choice. Most teachers felt that their students were comfortable with the group aspect of the activity due to the experience already gained in elementary and middle school classrooms.

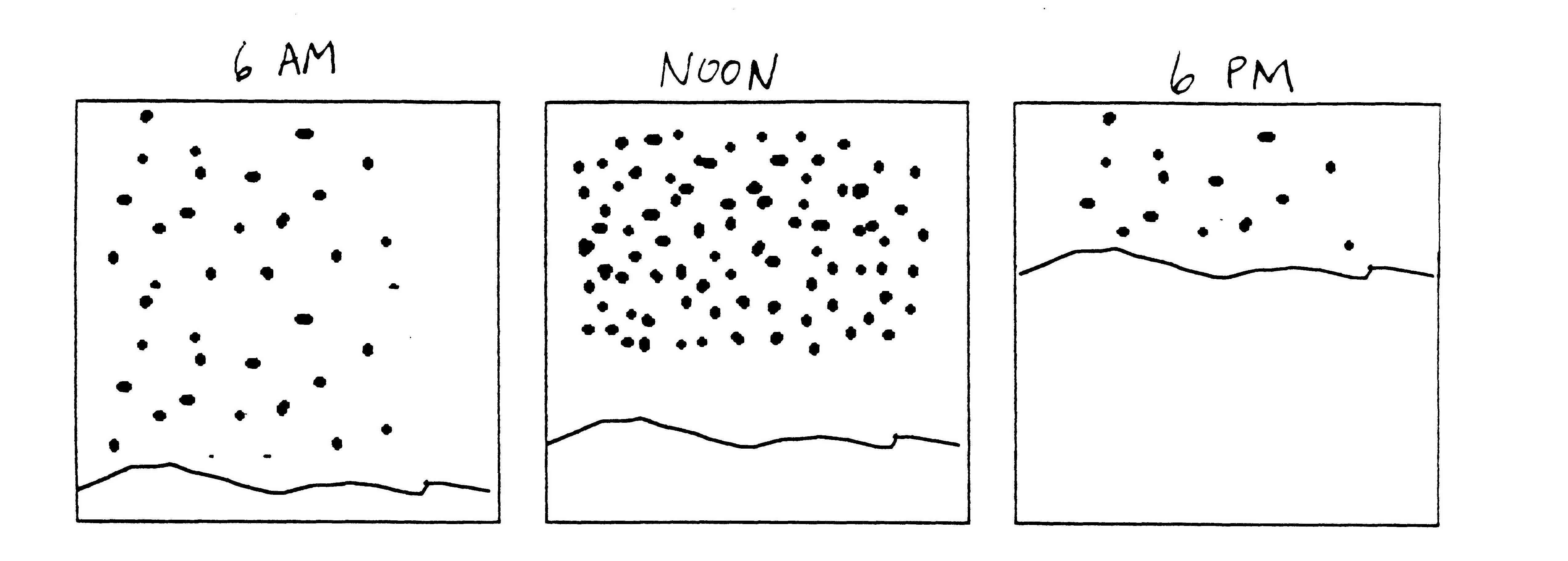
1. Explain how you would determine how much snow fell during the 12 hours from 6 AM to 6 PM on January 3. In your answer, list any additional information that would be helpful to know.
2. Calculate how much snow fell during the 12 hour period from 6 AM to 6 PM on January 3. Show your work and state the assumptions you made in finding your answer. Explain why those assumptions are reasonable.
3. Suppose you learned that more than half the snow fell between the hours of 10 AM and 2 PM. Determine whether or not your calculation in #2 is consistent with this new information.
4. Using the information in #3, calculate the amount of snow that fell during the 12 hour period from 6 AM to 6 PM on January 3. Describe how your method of calculation differs from the method you used in #2.

Some teams drew graphs that showed the snowfall rate increasing in a line from 0.5 to 2 inches and then decreasing back down to 0.5 in another line. The calculation of total snowfall was done by breaking the graph into two trapezoids or a triangle and rectangle. (see Diagram)

Other teams determined that the average snowfall rate was 1.25 inches, and therefore the total snowfall over 12 hours was 15 inches.

During the problem-solving exercise, very few teams considered a rate that wasn't linear. During a discussion later, Charlotte Trout's students agreed that given the variability of a snowstorm, a non-linear rate would have been reasonable.

Teachers had ideas for extensions of the problem or additional tasks. Ron Peterman changed the context of the problem to better fit his chemistry class by asking, "What if this were a precipitation reaction? Two solutions are poured together and slowly mix. The initial contact of the reagents gives precipitation at the rate of 0.5 gram per second. As they mix more completely, the rate goes to 2 grams per second; and after 6 seconds and as the reagents are used up, the rate drops to 0.5 gram per second." Linda Tinsman mentioned that her classes do an activity with absorption of visible light that could be framed as this type of problem. Several teachers concluded that open-ended tasks directly related to the curriculum would be valuable to the development of their students' problem-solving skills.