Using MATLAB to Solve a System of Equations
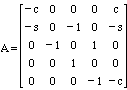 |
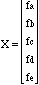 |
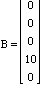 |
Invoke MATLAB and type the following: (Click here to download these commands as text)
n = 5; % n is the number of variables A = zeros(n,n); % A is first filled with zeros B = zeros(n,1); % B is filled with zeros angle = pi/4; % The angle is stored in radians s = sin(angle); % The coefficients are calculated c = cos(angle); A(1,1) = -c; % Enter in the non-zero elements of A and B A(1,5) = c; A(2,1) = -s; A(2,3) = -1; A(2,5) = -s; A(3,2) = -1; A(3,4) = 1; A(4,3) = 1; A(5,4) = -1; A(5,5) = -c; B(4,1) = 10; % The solution to A*X = B could be: X= inv(A)*B % This uses the inverse X= A\B % This uses Gaussian Elimination
These solutions will appear on the screen as text.
-7.0711 5 10 5 -7.0711
This code segment may be saved as a script file to be run again at a later time. The coefficient matrix could be entered into a data file with a text editor and then loaded into the program. The documentation with MATLAB explains those techniques.
Student Exercises
Exercises 1 - 8:
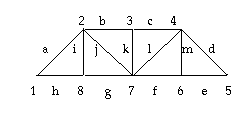
1. On the bridge above, a 10 ton vehicle is located at joints 6, 7, and 8. Find the forces on each member if joint 1 is fixed and all angles are 45 degrees.
Answer: Enter the following matrices into Matlab. c = cos 45 and s = sin 45.
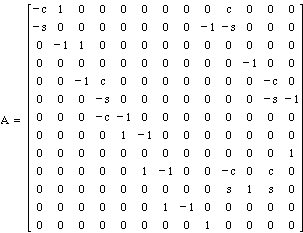 |
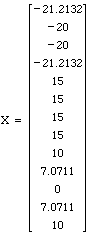 |
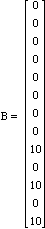 |
2. Suppose that the maximum force supported by each member is 20 tons.
If a single vehicle crosses the bridge without collapse, what is the maximum tonnage it may be?
Answer: 18.8 tons at joint 6 is the maximum force allowed.
3. Suppose the maximum force supported by each member
is 20 tons. If vehicles are located at joints 6, 7 and 8, what are their
maximum tonnages? Can the bridge hold more by spreading the forces over
the bridge or by concentrating most of the force in one place?
Answer: 9.4 tons at joints 6, 7 and 8 is supported by the bridge. Distributing the weight allows 28.2 tons total versus 18.8 tons at a single joint.
4. Suppose that the bridge is changed by using 40
degree angles at the bottom joints, rather than 45 degree angles. Place a
10 ton vehicle at joints 6, 7, and 8. What are the forces on the members
now?
Answer: c = cos 40 and s = sin 40 in the matrix for #1.
Also, use:
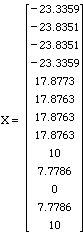
5. Using the changed bridge, suppose that the maximum force supported by each member is 20 tons. If a single vehicle crosses the bridge without collapse, what is the maximum tonnage it may be?
Answer: 17.1 tons at joint 6 is the maximum force allowed.
6. Using 50 degree angles at the bottom joints, place
a 10 ton vehicle at joints 6, 7, and 8. What are the forces on the
members?
Answer: c = cos 50 and s = sin 50 in the matrix for #1.
Also, use:
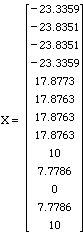
7. Using this bridge, suppose that the maximum force
supported by each member is 20 tons. If a single vehicle crosses the
bridge without collapse, what is the maximum tonnage it may be?
Answer: 20 tons since fm and fi must support the most downward force.
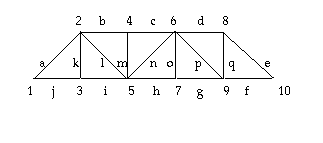
8. On
the bridge above, if forces of 10 tons are at joint 3, 15 tons at joint 5
and 10 tons at joint 9, find the forces on the members of the bridge.
Answer: Enter the following matrix in the Matlab program with c = cos 45 and s = sin
45
 |
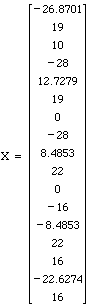 |
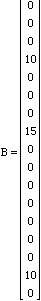 |
Continue on to the Background Information or back to the Bridge Model Main Page.