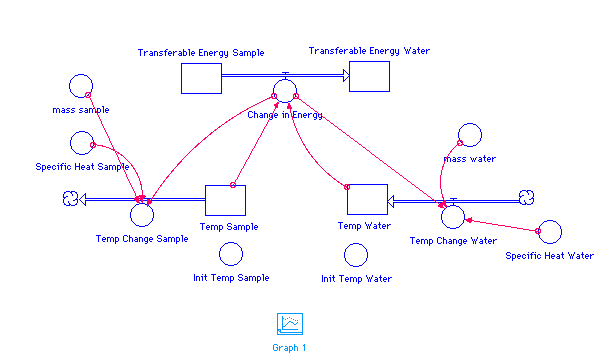
Temp_Sample(t) = Temp_Sample(t - dt) + (- Temp_Change_Sample) * dt
INIT Temp_Sample = Init_Temp_Sample
Temp_Change_Sample = Change_in_Energy/(mass_sample*Specific_Heat_Sample)
Temp_Water(t) = Temp_Water(t - dt) + (Temp_Change_Water) * dt
INIT Temp_Water = Init_Temp_Water
Temp_Change_Water = Change_in_Energy/(mass_water*Specific_Heat_Water)
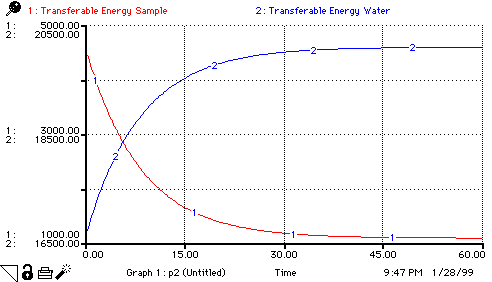
Transferable_Energy_Sample(t) = 
       Transferable_Energy_Sample(t - dt) + (- Change_in_Energy) * dt
INIT Transferable_Energy_Sample = 
       mass_sample*Init_Temp_Sample*Specific_Heat_Sample {J}
Change_in_Energy = 5*(Temp_Sample-Temp_Water)
Transferable_Energy_Water(t) = 
       Transferable_Energy_Water(t - dt) + (Change_in_Energy) * dt
INIT Transferable_Energy_Water = 
       mass_water*Specific_Heat_Water*Init_Temp_Water
Change_in_Energy = 5*(Temp_Sample-Temp_Water)
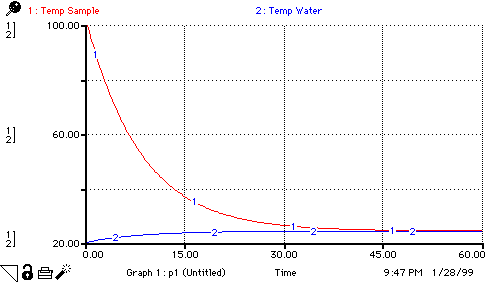
Init_Temp_Sample = 100
Init_Temp_Water = 20
mass_sample = 50 {g}
mass_water = 200 {g}
Specific_Heat_Sample = 0.89 {J/g C}
Specific_Heat_Water = 4.18 {J/g C}

Time Specs