As one would expect given the philosophy of System Dynamics, a number of "generic" or archetypical models have been postulated. The purpose of this exercise is to show some basic model types based on common graphs of relationships. The idea being, if your data generates one of these graphs, then the associated model will produce it in STELLA. One merely needs to substitute the names and values of the variables. To access a tutorial on the creation of the model, click on the link. Notice that while each type of model has at least two forms (ex. linear growth and decay) only one model is illustrated. It is left as an exercise for the reader to use the information to generate the equivalent model.
1. Linear Growth/Decay Model (Fisher) and Stimulus-Response Model (Hannon-Ruth)
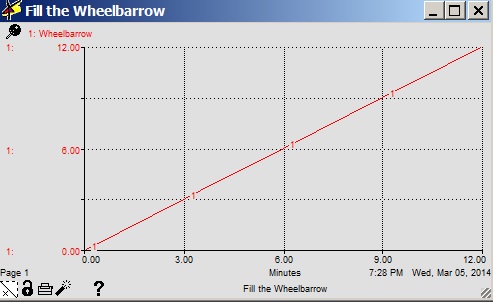
Inputs from the converter, and possibly from an external source, flow into the stock, independent of any feedback from the stock. For example, filling a wheelbarrow with dirt by the shovelful. As you would expect, this generates a straight line sloping to the upper right. 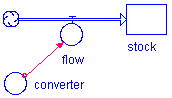
Linear Decay Model is quite similar with the exception of the direction of the flow, out from the stock rather than in to the stock. This causes the quantity in the stock to steadily decline. The graph is a straight line sloping down towards the right.
2. Exponential Growth/Decay Model (Fisher) and Self-Referencing Model (Hannon-Ruth)
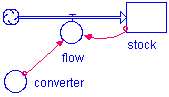
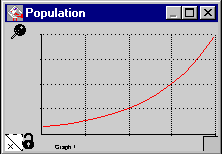
The salient feature of this model is that the Stock influences its own growth or decay. The notion of feedback is crucial in systems. This model forms the basis for many types of common systems from compounded interest to simple population models.
The generic formula is Flow = Stock * compounding fraction. The curve should look familiar.
3. Convergence Up/Down Model (Fisher) and Goal Seeking Model (Hannon-Ruth)
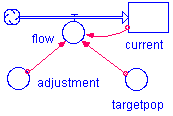
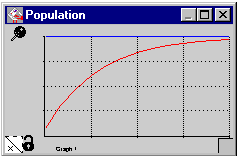
This model has a target population which the system is seeking to attain. It is basically the difference between the current state and the target goal which drives the system. The target can be either a stock (Fisher) or a converter (Hannon-Ruth).
The generic formula is Flow = (target - current) * adjustment fraction (converging upwards) or Flow = (current - target) * adjustment fraction (converging downwards).
Note that the two lines never meet.
4. Co-Flow Up/Down Model (Fisher)
This model is characterized by one stock rising or falling based upon the rising or falling of a second stock. This type of model is suitable for tracking how one quantity is interrelated with the fortunes of another quantity. The generic formula is: Tracking Flow = Primary Flow * Conversion Fraction.
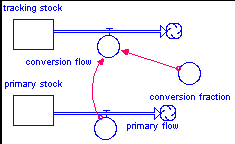
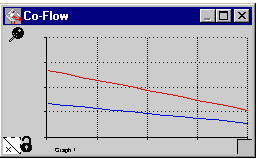
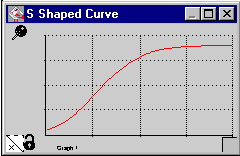
5. S-Shaped GrowthModel (Fisher)
The S Shaped curve is seen frequently in population models. It begins with exponential growth. At some point in the system, exponential decay takes over. These two competing forces balance out due to their interrelatedness...the decay factor is dependent upon the stock which is dependent upon the growth factor.
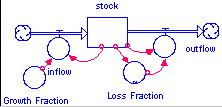
6. Overshoot & CollapseModel (Fisher)
This model is very similar to the S Shaped curve model. It differs in that equilibrium is never achieved and the decay continues. The equilibrium is not achieved because the decay factor is not relying on the same resource as the growth factor, each uses its own. However, the growth factor's resource (say population) is dependent on the decay factors resource (say food). The amount of food is initially large so few people die and the population grows. As the amount of food decreases, the number of number of people dying increases. Once the food reaches a certain threshold, the population collapses.
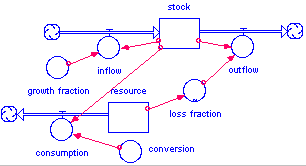
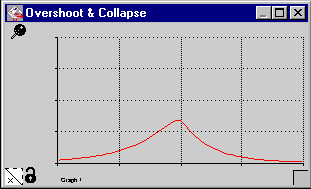
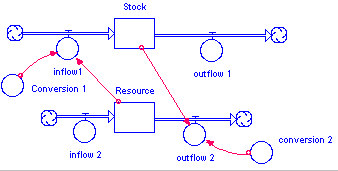
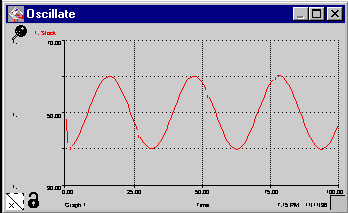
7. OscillationModel (Fisher)
Oscillation is similar to overshoot and collapse. Essentially it is an overshoot and collapse model which has a resource that can renew itself before total collapse occurs. There are two stocks, each of which has an inflow and an outflow. The stocks are connected to each other's flows, one to an inflow and one to an outflow. For this model to work properly, the inflow and outflow should be the same. A shock or jolt to the system sets off the oscillation with the size of the STEP function determining the amplitude of the oscillation.